Testy Jednorodności

Celem badania jednorodności jest stwierdzenie czy rozmieszczenie obiektów we Wszechświecie jest mniej więcej równomierne. Wykorzytuje się do tego obiekty najodleglejsze, które umożliwiają testowanie dużych obszarów obserwowanego Wszechświata. Jedną z metod badania jednorodności jest zliczanie obiektów w funkcji granicznej jasności obserwowanej. Przedstawiony zostanie teraz prosty model zliczeń nieruchomych obiektów rozmieszczonych ze stałą prędkością w jednorodnej przestrzeni.
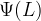- jest funkcją świecenia obiektów,
- F to minimalny strumień jaki obserwujemy od danego obiektu,
- r to odległość danego obiektu.
Wyznaczyamy ilość obiektów, których strumień jest większy od F. Aby było to możliwe ich jasność musi przekraczać 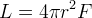. Aby wyliczyć ilość zliczeń należy scałkować to równanie po odległości:

%MATHMODE{N(\ge F)=\int^{\infty}_{0}4r^2 \int^{\infty}_{4\pi r^2F}\Psi(L)dL}%

Przekształcając tę całkę otrzymamy wynik stwierdzający, że ilość zliczeń jest proporcjonalna do strumienia w potędze -3/2

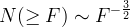
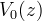Teraz postaramy się uogólnić tą metodę do obiektów znajdujących się w rozszeżającym się Wszechświecie. Wykorzystana zostanie tutaj zależność określana jako "obecna objętość" . Jest to objętość obszaru zajmowanego przez obiekty o przesunięciu ku czerwieni nie większemu niż z:

%MATHMODE{ \frac{dV_0}{dz}=(1+z)^3 \frac{dV}{dz}=4 \pi R^{2}(z) \frac{c}{H_0} \frac{1+z}{(1+ \Omega z)^{\frac{1}{2}}}}%

Zakładając, że mamy pewną próbkę obiektów o gęstości 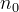otrzymujemy: %MATHMODE{dN=n_{0}\frac{dV_0(z)}{dz} dz}% Pozostaje jedynie tę wielkość podstawić pod naszą całkę i uprościć przy założeniu, że mamy do czynienia z jedną klasą obiektów o danej jasności i danym kącie nachylenia widma 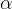oraz danej częstości obserwacji .

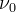%MATHMODE{L_{ \nu }=L_{0}(\frac{ \nu }{ \nu_{ 0 } })^{ - \alpha }}%

Następnie możemy określić strumień pochodzący od tego źródła o danym przesunięciu ku czerwieni z:

%MATHMODE{F= \frac{L_0}{4\piR^2(z)(1+z)^{3+ \alpha}}%

Dla obiektów z przestrzeni euklidesowaj wyrażenie się uprości i otrzymamy:

%MATHMODE{(\frac{dN}{dF})_E=-\frac{3}{2}\frac{n_0L_0^{\frac{3}{2}}}{6\pi^\frac{1}{2}}F^{-\frac{5}{2}}}%

Ostatecznie w modelu kosmologicznym mamy:

%MATHMODE{\frac{dN}{dF}=\frac{\frac{dN}{dz}}{\frac{dF}{dz}}}%

Dla ekspandującego Wszechświata liczba słabych źródeł powinna być mniejsza niż w przypadku nieruchomych obiektów w płaskiej przestrzeni. Przeczą temu obserwacje zatem założenie związane z brakiem ewolucji radioźródeł jest błędne. Należy przyjąć, że w przeszłości były one liczniejsze lub jaśniejsze. Nie umożliwia to jednak określenia parametrów modelu kosmologicznego ponieważ nie mamy informacji związanych z tempem ich ewolucji.

---

Literatura

[1] Michał Jaroszyński, "Galaktyki i budowa Wszechśwata", PWN, 1993
[2] "Astronomia Popularna", praca zbiorowa, WP, 1990

Internet

Przejawy obecności pola kwintesencji w modelach kosmologicznych