Jednym z sukcesów teorii Wielkiego Wybuchu jest to, iż dobrze ona tłumaczy obserwowane obfitości pierwiastków we Wszechświecie. Mianowicie kiedyś sądzono że wszystkie gwiazdy pierwotnie były zbudowane z wodoru, a inne cięższe pierwiastki tworzyły się w nich na zasadzie reakcji jądrowych. Dziś jednak wiemy że procesy takie byłyby mało efektywne. Pierwiastki takie jak , , 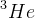, 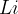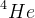nie mogły powstać w ten sposób. I tutaj pojawia się nukleosynteza jako odpowiedź na pytanie o obfitość pierwiastków we Wszechświecie.

W czasie ekspansji Wszechświat zwiększał swoje rozmiary, malała gęstość i spadała energia kinetyczna cząsteczek. Gdy osiągnęła ona poziom około 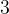MeV (odpowiadało by to temperaturze około 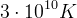i czasowi istnienia Wszechświata około 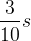), z powodu spadku energii cząsteczek poniżej wspomnianej wartości, nastąpiło wtedy zerwanie kontaktu między 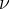(neutrinami) a materią. Przed tym wydarzeniem neutrina, materia (tu rozważamy elektrony ) i 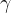(fotony) były w stanie równowagi, ich temperatury były sobie równe:

%MATHMODE{T_e=T_\gamma=T_\nu \qquad (1)}%

w takich równowagowych warunkach zachodziły reakcje anihilacji i kreacji:

%MATHMODE{\nu_e + \widetilde{\nu_e} \rightleftharpoons e^+ + e^- \qquad (2)}% %MATHMODE{\gamma + \gamma \rightleftharpoons e^+ + e^- \qquad (3)}%

Jako że istnieją trzy rodziny neutrin ( elektronowa, mionowa i taonowa) do relacji tych należy dodać:

%MATHMODE{\nu_\mu + \widetilde{\nu_\mu} \rightleftharpoons \mu^+ + \mu^- \qquad (4)}% %MATHMODE{\nu_\tau + \widetilde{\nu_\tau} \rightleftharpoons \tau^+ + \tau^- \qquad (5)}% %MATHMODE{\gamma + \gamma \rightleftharpoons \mu^+ + \mu^- \qquad (6)}% %MATHMODE{\gamma + \gamma \rightleftharpoons \tau^+ + \tau^- \qquad (7)}%

Po spadku energii poniżej wspomnianego poziomu reakcja którą opisuje wzór (2) przestaje praktyczne zachodzić lecz relacja (1) zachowuje swą ważność z uwagi na to, że temperatury te zależą od tempa ekspansji Wszechświata. Chwila w której następuje zerwanie kontaktu między neutrinami a materią uznaje się za moment powstania TŁA NEUTRINOWEGO, jest to zjawisko podobne do powstania CMB.

Ekspansja Wszechświata jest silnym czynnikiem przeszkadzającym w kontaktach między cząstkami, im jej tempo jest większe, tym szybciej następuje zerwanie kontaktu między nimi. Do czasu gdy spełnione jest kryterium na równowagowy przebieg poszczególnego procesu, czyli:

%MATHMODE{\Gamma_X(z) \ \textgreater \ \Gamma_H(z) \qquad (8)}% %MATHMODE{\Gamma_H \equiv \frac{1}{t_H} \qquad (9)}%

gdzie:

- redshift

- dynamiczny wiek Wszechświata

cząstki mogą się swobodnie kontaktować i ustala się stan równowagi, lecz gdy to kryterium przestanie być spełniane warunki panujące w ośrodku ulegną zamrożeniu, jak to ma miejsce w przypadku neutronów i protonów. Czas połowicznego rozpadu dla protonów i neutronów wynosi odpowiednio:

%MATHMODE{p: \qquad \tau_{\frac{1}{2}} \gg t_0 \qquad (10)}% %MATHMODE{n: \quad \tau_{\frac{1}{2}} \approx 889 s \qquad (11)}%

gdzie:

- wiek Wszechświata () dla stałej Hubble'a równej

wynika z tego że po pewnym czasie, na skutek rozpadu 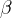(relacja (13) strzałka ) liczba protonów staje się większa od liczby neutronów. Tak w istocie się dzieje. Do czasu gdy:

%MATHMODE{E_K \gg 1MeV \qquad (12)}%

tempo kreacji neutronów równa się tempu rozpadu 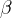czyli 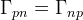, lecz gdy energia kinetyczna cząstek spada do poziomu 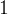MeV (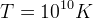, ), moment ten przypada na koniec ERY LEPTONOWEJ, i tempo ekspansji Wszechświata przewyższy tempo kreacji neutronów 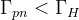przestanie być spełnione kryterium na równowagowy przebieg procesu więc .

%MATHMODE{n \rightleftharpoons p + e^- + \widetilde{\nu_e} \qquad (13)}% %MATHMODE{n + e^+ \rightleftharpoons p + \widetilde{\nu_e} \qquad (14)}% %MATHMODE{n + \nu_e \rightleftharpoons p + e^- \qquad (15)}%

Jest to moment w którym neutrony i protony po raz ostatni mogły oddziaływać ze sobą w sposób równowagowy. Stosunek ich ilości wynosi:

%MATHMODE{\frac{n_n}{n_p} = \Biggl\{ \ {(\frac{m_n}{m_p})^{\frac{3}{2}}=1 \qquad ;\ E_K \gg 1MeV \atop 0 \qquad \qquad ;\ E_K \rightarrow 0} \qquad (16)}%

Z tej zależności wyraźnie widać że liczba neutronów dąży do zera, w wyniku czego może okazać się że ostatecznie we Wszechświecie pozostaną same protony. Aby tego uniknąć zanim wszystkie neutrony ulegną rozpadowi należy je związać w jądra pierwiastków, tutaj jako ratunek dla neutronów pojawia nukleosynteza. W rzeczywistości stosunki obfitości dla końca ery leptonowej i początku nuleosyntezy ustalają się odpowiednio na poziomach: .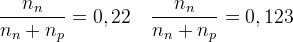

W chwili gdy energia spadnie do 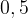MeV (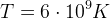, t = kilka sekund) z uwagi na to, że 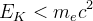, czyli energia kinetyczna elektronów spadnie poniżej energii spoczynkowej następuje zerwanie równowagi pomiędzy kreacją (relacja (18)) a anihilacją (relacja (17)) par 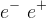(elektron - pozyton).

%MATHMODE{e^- + e^+ \rightarrow \gamma +\gamma \qquad (17)}% %MATHMODE{\gamma +\gamma \rightarrow e^- + e^+ \qquad (18)}%

Od tej chwili kreacja praktycznie przestaje mieć znaczenie. Do ogromu fotonów, na jeden barion (proton, neutron) przypada ich około miliard, dochodzą kolejne powstałe z anihilacji elektronów i pozytonów. Relacja (1) przestaje być słuszna. Od tej chwili 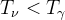. Od teraz zachodzić będzie relacja:

%MATHMODE{T_\nu =\Big(\frac{4}{11}\Bigr)^{\frac{1}{3}} T_\gamma \qquad (19)}%

co w chwili obecnej daje 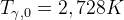oraz .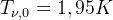

Dalszy bieg wydarzeń jest następujący. Proces nukleosyntezy zacznie się gdy energia protonów i neutronów spadnie do poziomu energii wiązania deuteru, która wynosi 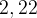MeV. W rzeczywistości z uwagi na dużą liczbę fotonów, których widmo promieniowania ma charakter plankowski, poziom ten należy obniżyć do wartości około 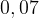MeV. Wynika to z tego że wysokoenergetycznych fotonów jest wystarczająco dużo by rozbić jądro deuteru. Opisuje to wzór określający wystarczającą temperaturę potrzebną do rozbicia danego wiązania:

%MATHMODE{T = \frac{T_W}{-\ln \eta} \qquad (20)}%

gdzie:

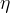- stosunek liczby barionów do fotonów jest to wartość stała w trakcie ekspansji Wszechświata i wynosi 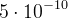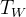- temperatura wiązania (można ją zamiennie stosować z energią, gdyż 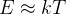, 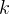- stała Boltzmanna )

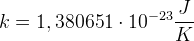Gdy energia cząstek osiągnie wspomnianą wartość rozpocznie się proces NUKLEOSYNTEZY (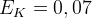 MeV, 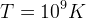, 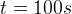). Jej główne łańcuchy to:

%MATHMODE{n + p \rightarrow D +\gamma \qquad (21)}% %MATHMODE{D + D \rightarrow \Biggl\{ \ {^3He + n \atop \quad T + p } \qquad (22)}% %MATHMODE{n + D \ \rightarrow \ \quad T + \gamma \qquad (23)}% %MATHMODE{p + D \ \rightarrow \ ^3He + \gamma \qquad (24)}% %MATHMODE{p + T \ \rightarrow \ ^4He + \gamma \qquad (25)}% %MATHMODE{D + T \ \rightarrow \ ^4He + n \qquad (26)}% %MATHMODE{D + \ ^3He \ \rightarrow \ ^4He + p \qquad (27)}% %MATHMODE{n + \ ^3He \rightarrow \Biggl\{ \ {\quad T + p \atop ^4He + \gamma } \qquad (28)}% %MATHMODE{^3He \ + \ ^3He \ \rightarrow \ ^4He + 2p \qquad (29)}%

gdzie:

- deuter

- tryt

oraz pierwiastki śladowe:

%MATHMODE{^4He \ + T \ \rightarrow \ ^7Li + n \qquad (30)}% %MATHMODE{^4He \ + \ ^3He \ \rightarrow \ ^7Be + \gamma \qquad (31)}%

Nukleosynteza praktycznie kończy się na 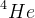jako głównym produkcie BBN, hel tworzy większość neutronów i odpowiadająca im liczba protonów. Proces (relacja (21)) jest swoistym wąskim gardłem z uwagi na to że deuter szybko ulega zniszczeniu. Reszta materii to 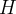czyli pojedyncze protony. Wynik nukleosyntezy przedstawia się następująco:

%MATHMODE{X_4 = \frac{n(^4He)}{n(H)} \approx \frac{1}{12} \qquad (32)}% %MATHMODE{Y_4 = 2 \cdot \frac{n_n}{n_n + n_p} = 0,246 \pm 0,0014 \qquad (33)}% %MATHMODE{\frac{D}{H} = (3,4 \pm 0,5) \cdot 10^{5} \qquad (34)}% %MATHMODE{\frac{^7Li}{H} = (3,5 \pm 1) \cdot 10^{-10} \qquad (35)}%

gdzie:

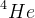- ilościowa obfitość w stosunku do 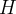(czyli liczby protonów)

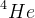- masowa obfitość w stosunku do

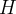Wynika stąd że 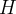oraz 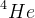dominują we Wszechświecie. Nukleosynteza zostaje przerwana gdy energie cząstek stają się zbyt małe by pokonać barierę potencjału. Dzieje się to gdy ( 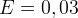MeV, 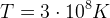, 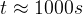). Wtedy to wzajemne stosunki obfitości pierwiastków zostają zamrożone, zmniejsza się tylko liczba ocalałych neutronów n skutek rozpadu 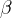. Obfitość i 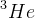w stosunku do 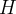zależą od 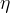czyli w praktyce od 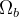, czyli bezwymiarowej gęstości barionów.

%MATHMODE{\Omega_b = \frac{\rho_b}{\rho_{kryt}} \qquad (36)}% %MATHMODE{\rho_{kryt}= \frac{3 H^2}{8 \pi G} \qquad (37)}%

gdzie:

- gęstość wszystkich składników Wszechświata (relatywistycznych i nierelatywistycznych), wyliczona z 1 równania Friedmanna przy założeniu że krzywizna Wszechświata wynosi 0. Jest to parametr określający jego kształt

Na chwilę obecną 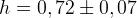wygląda to następująco:

%MATHMODE{h = \frac{H_0}{100 \frac{km}{s \cdot Mpc}} \qquad (38)}% %MATHMODE{\rho_{kryt,0} = 0,97 \cdot 10^{-29} \frac{g}{cm^3} \qquad (39)}% %MATHMODE{\rho_{m,0} = 3 \cdot 10^{-30} \frac{g}{cm^3} = \frac{3}{10} \rho_{kryt,0} \qquad (40)}% %MATHMODE{\rho_{r,0} = 4,4 \cdot 10^{-34} \frac{g}{cm^3} \qquad (41)}% %MATHMODE{\rho_{b,0} = (3,6 \pm 0,4) \cdot 10^{-31} \frac{g}{cm^3} \approx \frac{1}{10} \rho_{m,0} \qquad (42)}%

Potwierdzają to obserwacje obfitości deuteru za pomocą absorpcji światła kwazarów w trakcie jego przechodzenia przez obłoki pierwotnego gazu. Mamy stąd:

%MATHMODE{0,016 \leq \Omega _b h^2 \leq 0,024 \qquad (43)}%

Na obfitości pierwiastków mają wpływ tylko dwa parametry:

- Liczba rodzin neutrin, zwiększenie ich ilości spowodowało by szybszą ekspansję Wszechświata a przez co wpłynęło by na inne stosunki ilościowe pierwiastków, do czasu nukleosyntezy zachowało by się więcej neutronów przez co powstało by więcej 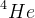- Podobny wpływ ma zwiększenie gęstości materii barionowej.

Zgodność z obserwacjami uzyskuje się gdy , zaś mierzona obfitość litu 7 skłania nas do uznania że , co przy wcześniej zadanym daje , a więc - czyli resztę materii stanowi tzw. Ciemna materia, której obecność postuluje się badając krzywe rotacji galaktyk.

Bibliografia: zobacz biblio na NiestabilnoscGrawitacyjna

-- RoWia - 26 Feb 2004