You are here: Foswiki>Main Web>TWikiUsers>AndrzejCzarny>SredniaGestosc (13 Jun 2005, BoudRoukema)EditAttach
Średnia gęstość
Poniższa metoda zakłada, że gęstość Wszechświata można ocenić na podstawie jasności materii jaka się w nim znajduje. Zadaniem będzie ustalenie średniego stosunku masy do jasności. Wykorzystamy do tego celu funkcję świecenia galaktyk n(L). Określa ona liczbę galaktyk o jasności z przedziału od L do L+dL w jednostce objętości [1]. Najdogodniejszą formułę podał Schechter: %MATHMODE{n(L)=\frac{n_*}{L_*}[\frac{L}{L_*}]^{-\alpha}e^{-\frac{L}{L_*}}}% Wykładnik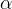
został dobrany na podstawie badań słabych galaktyk na wartość 5/4. Zakłada ona, że bardzo słabe galaktyki mają nieskończoną gęstość, ale gęstość źródeł światła pozostaje skończona:
%MATHMODE{L_V=\int^\infty_0 n(L)LdL \approx 2\cdot 10^8 hL_{\odot} Mpc^{-3}}%
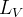określa jasność wszystkich galaktych w jednostce objętości. Potrzebny jest także średni stosunek masy do jasności 
. Wprowadźmy bezwymiarowy parametr gęstość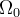 
:
%MATHMODE{\Omega_0=\frac{<\frac{M}{L}>L_V}{\rho_c}}%
Obserwacje wykazały, że średni stosunek masy do jasności jest tym większy im za galaktykę przyjmuje się większy obszar wokół centrum.
Dla gęstości krytycznej Wszechświata przyjmuje on postać:
%MATHMODE{<\frac{M}{L}>_c=1350h M_{\odot}/L_{\odot}}%
W naszych rozważaniach przyjmujemy za typowy stosunek masy do jasności, taki jak w parach i grupach galaktyk 
. Spowoduje to, że nasz bezwymiarowy parametr gęstości przyjmie postać 
.
Ocena ta jest związana z promieniem ciemnych otoczek wokół galaktyk o ile są one proporcjonalne do obszarów świecących [1].Rozpatrując ten problem inaczej możemy przyjąć, że
przy założeniu, że mamy pewną liczbę galaktyk eliptycznych f oraz odpowienio galaktyk spiralnych 1-f. Możemy wyznaczyć charakterystyczne masy galaktyk, korzystając z formuły Schechtera oraz ograniczając od dołu rozmiary ciemnych otoczek. Założenia te dają oszacowanie na masy galaktyk eliptycznych i spiralnych. Pamiętając, że galaktyki eliptyczne stanowią 1/3 wszystkich galaktyk [1] otrzymujemy średnią gęstość wszechświata.
W ostateczności otrzymujemy :
%MATHMODE{\Omega_0=0.0017R}%
gdzie R jest promieniem otoczki ciemnej materii wyrażonym w jednostkach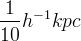 
.
Literatura
[1]. Michał Jaroszyński, "Galaktyki i budowa Wszechśwata", PWN, 1993Ciekawe Linki
KOSMOLOGIA — wybrane zagadnienia (prof. Jerzy Sikorski)Czy otoczek ciemnej materii to core radius in the density profile of elliptical galaxies? -- BoudRoukema - 13 Jun 2005
Error during latex2img:
ERROR: problems during latex
INPUT:
\documentclass[fleqn,12pt]{article}
\usepackage{amsmath}
\usepackage[normal]{xcolor}
\setlength{\mathindent}{0cm}
\definecolor{teal}{rgb}{0,0.5,0.5}
\definecolor{navy}{rgb}{0,0,0.5}
\definecolor{aqua}{rgb}{0,1,1}
\definecolor{lime}{rgb}{0,1,0}
\definecolor{maroon}{rgb}{0.5,0,0}
\definecolor{silver}{gray}{0.75}
\usepackage{latexsym}
\begin{document}
\pagestyle{empty}
\pagecolor{white}
{
\color{black}
\begin{math}\displaystyle <\frac{M}{L} >\end{math}
}
\clearpage
{
\color{black}
\begin{math}\displaystyle <\frac{M}{L}> \sim L^{1/4}\end{math}
}
\clearpage
{
\color{black}
\begin{math}\displaystyle <{\frac{M}{L}}>\approx 700 M_{\odot}\end{math}
}
\clearpage
{
\color{black}
\begin{math}\displaystyle \Omega_0\approx 0.1\end{math}
}
\clearpage
\end{document}
STDERR:
This is pdfTeX, Version 3.141592653-2.6-1.40.24 (TeX Live 2022/Debian) (preloaded format=latex)
restricted \write18 enabled.
entering extended mode
(/tmp/FHQUrSnv71/P1EXj364Nb
LaTeX2e <2022-11-01> patch level 1
L3 programming layer <2023-01-16>
(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2022/07/02 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/fleqn.clo)
(/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
(/usr/share/texlive/texmf-dist/tex/latex/xcolor/xcolor.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/color.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/dvips.def)
(/usr/share/texlive/texmf-dist/tex/latex/graphics/mathcolor.ltx))
(/usr/share/texlive/texmf-dist/tex/latex/base/latexsym.sty)
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-dvips.def)
No file P1EXj364Nb.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ulasy.fd)
! Misplaced alignment tab character &.
l.17 \begin{math}\displaystyle &
lt;\frac{M}{L} >\end{math}
! Misplaced alignment tab character &.
l.17 \begin{math}\displaystyle <\frac{M}{L} &
gt;\end{math}
[1]
! Misplaced alignment tab character &.
l.22 \begin{math}\displaystyle &
lt;\frac{M}{L}> \sim L^{1/4}\end{math}
! Misplaced alignment tab character &.
l.22 \begin{math}\displaystyle <\frac{M}{L}&
gt; \sim L^{1/4}\end{math}
[2]
! Misplaced alignment tab character &.
l.27 \begin{math}\displaystyle &
lt;{\frac{M}{L}}>\approx 700 M_{\odot}\en...
! Misplaced alignment tab character &.
l.27 \begin{math}\displaystyle <{\frac{M}{L}}&
gt;\approx 700 M_{\odot}\en...
[3] [4] (./P1EXj364Nb.aux) )
(see the transcript file for additional information)
Output written on P1EXj364Nb.dvi (4 pages, 1532 bytes).
Transcript written on P1EXj364Nb.log.
Edit | Attach | Print version | History: r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r3 - 13 Jun 2005, BoudRoukema
Cosmo |
|
Copyright © CC-BY-SA by the contributing authors. All material on this collaboration platform is copyrighted under CC-BY-SA by the contributing authors unless otherwise noted. Ideas, requests, problems regarding Foswiki? Send feedback